Research

• Multi-Dimensional Teacher Effects (working paper)

  It is now established that teacher quality, as measured by short-term test scores, is an important contributor to meaningful long-term student outcomes like income and educational attainment. However, easily-measurable short-term outcomes may be a poor proxy for meaningful long-term outcomes if teachers' effects go beyond what can be easily captured by test scores. In this paper, I demonstrate that high school graduation and long-term attendance and test scores cannot be predicted well by short-term effects. For example, even if teacher effects on contemporaneous outcomes were perfectly measured, they would only explain about 3% of the variation in teacher effects on high school graduation.

  I use data from New York City public schools to estimate the covariance structure of teacher effects on several outcomes: present and future test scores, present and future attendance, and high school graduation. Studying the covariance matrix of teacher effects reveals the magnitude of teacher effects on each outcome and the relationship between teacher effects on different outcomes while sidestepping the need to estimate individual teacher effects.

  Teachers have substantial effects on high school graduation, and on test scores and attendance four years in the future. Students of a teacher one standard deviation above average at improving graduation rates are 5 percentage points more likely to graduate high school. Although teacher quality is an important determinant of the long-term effects I observe, long-term effects cannot be predicted well by short-term effects. My results also suggest that teacher effects on attendance could be an important supplement to score-based measures of teacher value-added, since teachers. who improve attendance tend to improve high school graduation rates, while attendance effects are only weakly correlated with test score effects. I also use Principal Components Analysis to show that the correlation matrix of teacher effects can be well-represented by three easily interpretable components.

  

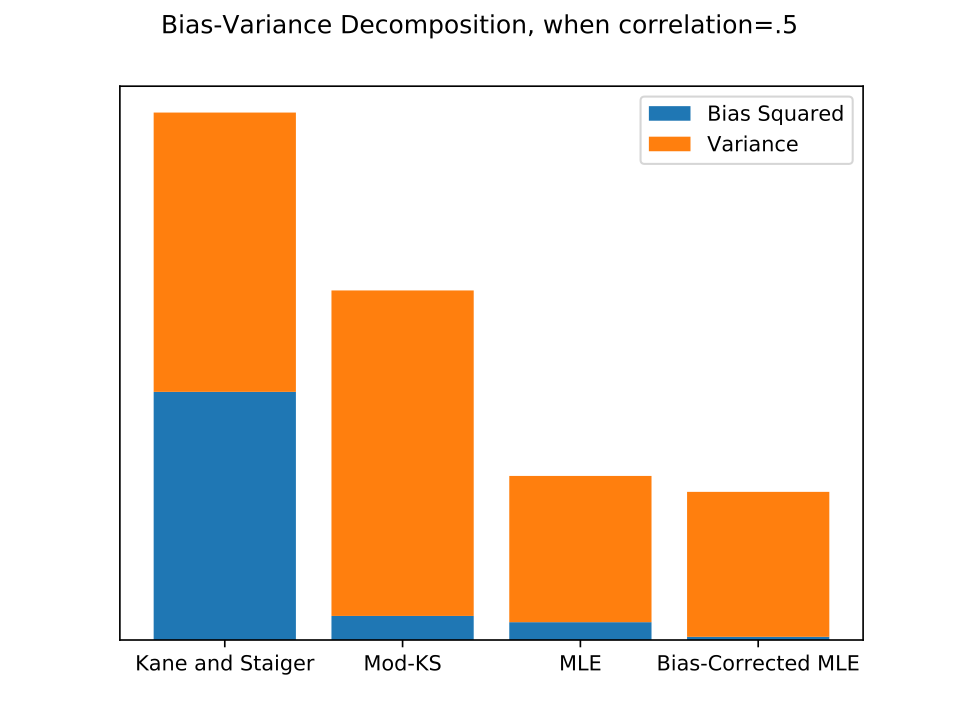
• Which Value-Added Estimator Works Best and When? (working paper)

  As value-added estimation spreads to fields outside education, where data sets may be small and experimental validation infeasible, estimators that perform well without millions of observations are increasingly needed. I clarify conditions under which existing methods are identified, sign their biases, and derive asymptotic standard errors, and I develop a likelihood-based estimator. Monte Carlo experiments show that the the likelihood-based estimator nearly eliminates bias without increasing variance, and that confidence intervals based on the asymptotic distribution of the estimator give approximately correct but slightly anti-conservative coverage probabilities. I compare results from each estimator on two real datasets: data on elite bureaucrat postings and local economic activity in India, and a dataset of eighth grade math teachers and test scores in New York City.

  

• Bureaucrat Value Added: The Effect of Individual Bureucrats on Local Economic Outcomes in India, with Jonas Hjort and Gautam Rao. Working paper coming soon!

  We use several value-added estimators to study a question relevant to political economy: How much agency do individual bureaucrats have to impact local economic performance? We study high-ranking bureaucrats in the Indian Administrative Service, India's national bureaucracy. These bureaucrats, District Collectors, District Collectors, who are quasi-randomly assigned to manage the bureaucracy of an Indian district and often transfer to different districts in the same state. This setting presents econometric challenges, since we have relatively few observations and high-dimensional covariates. By randomly permuting bureaucrat names, we show that value-added estimators have strong finite-sample biases in this setting. Point estimates suggest that variance in District Collector quality accounts for substantial variance in project completion and night light intensity. However, randomization inference shows that our estimates are in fact insignificant.